If you're here, I assume you know what Sudoku is. One common challenge for modern programmers is a solver for Sudoku puzzles, reminiscent of classic programming hacks like the iterative "Guess the Number" game or "99 Bottles of Beer".
In 2011, I was interviewing for (and landing) a new job. It would involve C# LINQ programming, which was new to me at the time. LINQ is made up of many set-based operators and commands, so a Sudoku solver seemed like a great way to practice and experiment with the capabilities.
There are many Sudoku solvers on the web, of course. Peter Norvig's solution is particularly elegant. Please read that first, as that discussion covers most of the basics and forms a starting point for my work here. Mr. Norvig sets out a particularly elegant algorithm of constraint propagation. But his Python is mostly a foreign language to me, so it'll be up to me to take the description and implement it in C#. I'm also going to expand past a simple solver to include a generator.
First off, I'm dispensing with Peter Norvig's notion of "A1" style cell references and string storage. My goal here is to explore LINQ set-based operations, so I'm storing the puzzle as a flat sequential array of 81 elements. A two-dimensional 9 x 9 array might be more intuitively obvious, but we'll see that operations are simpler if we can work on the entire puzzle as one flat region. So the sequence of 81 elements reads left-to-right and top-to-bottom as you would expect.
0 1 2 | 3 4 5 | 6 7 8 9 10 11 | 12 13 14 | 15 16 17 18 19 20 | 21 22 23 | 24 25 26 ---------+----------+--------- 27 28 29 | 30 31 32 | 33 34 35 36 37 38 | 39 40 41 | 42 43 44 45 46 47 | 48 49 50 | 51 52 53 ---------+----------+--------- 54 55 56 | 57 58 59 | 60 61 62 63 64 65 | 66 67 68 | 69 70 71 72 73 74 | 75 76 77 | 78 79 80
What is each of those elements? As Peter demonstrates, the fundamental structure of a Sudoku solve-in-progress can be described as a list of possible candidates for each cell. So each element is itself an array of integers. Let's define that, and a few constructors to initialize it.
class SudokuPuzzle
{
public int[][] Cells;
public int Length;
public int BoxSize { get { return (int)Math.Sqrt(Length); } }
public SudokuPuzzle(int n)
{
Cells = Enumerable.Repeat(Enumerable.Range(1, n).ToArray(), n * n).ToArray();
Length = n;
}
public SudokuPuzzle(SudokuPuzzle p)
{
Cells = p.Cells.Select(c => c.ToArray()).ToArray();
Length = p.Length;
}
}
The first constructor simply sets up a puzzle of the specified size with no constraints. The inner expression Enumerable.Range(1, n) creates an integer sequence of {1 2 3 4 5 6 7 8 9}. The outer function Enumerable.Repeat creates nē copies of it. So now we have 81 cells each containing all 9 candidates. That was done by a very compact LINQ expression, not at all like you'd see in older imperative C-family languages with nested for loops.
The second constructor implements a deep-copy of a SudokuPuzzle object to a new one. The inner c.ToArray() creates a copy of a cell's list of candidates, with the outer Select(...).ToArray() applying that to each element of Candidates. We will use this later.
Next we define the notion of peers. A pair of Sudoku cells are peers if they exist in the same row or same column or same box as each other. They can "see" each other so cannot have the same value when solved. Mr. Norvig expressed this thought with some string cross-product manipulation in Python, but I want to do it with all integers and LINQ operations.
public bool IsPeer(int c1, int c2)
{
return (c1 / Length == c2 / Length //Cells in same row
|| c1 % Length == c2 % Length //Cells in same column
|| (c1 / Length / BoxSize == c2 / Length / BoxSize && c1 % Length / BoxSize == c2 % Length / BoxSize)) //Cells in same box
&& c1 != c2; //Cell is not peer to itself
}
public int[] Peers(int cell)
{
return Enumerable.Range(0, Length * Length).Where(c => IsPeer(cell, c)).ToArray();
}
First we define a function that answers the simple question "Are these two cells peers?" by doing a bit of math with the cell indexes. Armed with that, the Peers function can very simply return the list of cell indexes that are peers to a requested cell. Start with a list of every possible cell in the puzzle as Enumerable.Range(0, Length * Length) , and filter it as you see there, using IsPeer in the lambda expression of the Where clause.
(Note that these peer operations are not static methods. They are dependent on the defined size of the puzzle. One enhancement I'm making over Peter Norvig's solution is that the puzzle size is fully flexible, not hardcoded to 9x9.)
class SudokuPuzzleTests
{
public static void TestPeers()
{
var p = new SudokuPuzzle(9);
var peers = p.Peers(40);
var expectedResult = new int[] { 4, 13, 22, 30, 31, 32, 36, 37, 38, 39, 41, 42, 43, 44, 48, 49, 50, 58, 67, 76 };
Debug.Assert(peers.SequenceEqual(expectedResult));
}
}
A quick test method shows that it works as expected, returning all the peers for the center cell of the puzzle. The LINQ function SequenceEqual expresses that test concisely, no need to write a loop through the arrays comparing each value.
Now we're ready for the main logic. I'm going to diverge somewhat from Peter Norvig's approach. He defines the fundamental operation as eliminating a candidate from the cell, and defines placing a value in terms of eliminating all other candidates. I think the code follows a more intuitive design if placing a value in a cell is the central operation. So here we go with a PlaceValue function, which can be used both for search-and-backtrack solving and for initially populating the puzzle from a set of clues.
public static SudokuPuzzle PlaceValue(SudokuPuzzle input, int cellIndex, int value)
{
var puzzle = new SudokuPuzzle(input);
if (!puzzle.Cells[cellIndex].Contains(value))
return null;
puzzle.Cells[cellIndex] = new int[] { value };
var CellsToPlace = new Dictionary<int, int>();
//Remove this value from the candidate list of all its peers
foreach (int peerIndex in puzzle.Peers(cellIndex))
{
var newPeers = puzzle.Cells[peerIndex].Except(new int[] { value }).ToArray();
//If this operation reduced a cell to zero candidates, that is a contradiction and this call to PlaceValue cannot lead to a solution.
if (!newPeers.Any())
return null;
//If this operation reduced a cell from more than one candidate to exactly one candidate, we will later recurse on PlaceValue with it
if (newPeers.Length == 1 && puzzle.Cells[peerIndex].Length > 1)
CellsToPlace.Add(peerIndex, newPeers.Single());
puzzle.Cells[peerIndex] = newPeers;
}
foreach (var cell in CellsToPlace)
{
if ((puzzle = PlaceValue(puzzle, cell.Key, cell.Value)) == null)
return null;
}
return puzzle;
}
The first thing PlaceValue does is create a deep copy of the puzzle. This is a pure function; the input SudokuPuzzle object is treated as immutable. (If this were Java, we'd apply the final keyword to that argument, but C# lacks that capability.) All our work will be done on this copy. So if we encounter an impossible situation, this function just returns null and lets its caller continue using its previous puzzle object. Next we have a sanity check, making sure that we're not trying to place a value in a cell from which it's already been eliminated. (This should never happen.) Then we actually place the value in the cell, by assigning it a new list of only one candidate. Then in the foreach loop, we eliminate this value from the candidate list of all its peers, checking to see if any peer got reduced to zero candidates indicating a contradiction.
The slightly tricky bit here is the last loop operating on the dictionary I've defined as CellsToPlace. Our data structure does not distinguish whether a cell with a single candidate had that value deliberately placed or was simply reduced to a single candidate by the action of a peer. This can lead to a contradiction, best illustrated with an example. Suppose three adjacent cells have their remaining candidates as {7 8} {7 9} {7 9}. And suppose we try to place 7 in the first cell of the three. Now the other two cells each have 9 as their only remaining candidate, but that cannot be a solution. How do we detect this? My answer is that whenever a cell is reduced to one and only one candidate, recursively call PlaceValue on THAT cell. So in this example, we would place 7 in the first cell, 9 in the next cell, and discover the contradiction on removing the last possible candidate from the third cell.
Human Sudoku players would recognize the {7 8} {7 9} {7 9} case as naked twins, and preemptively eliminate 7 from the first cell. A computational Sudoku solver could do the same thing if we wanted, but it's just not necessary as we can cover that case with more generalized logic.
So now we have the ability to place a value in a cell, and either detect a contradiction or return a copy of the puzzle with that value placed and all of the tumbling consequences. The final piece we need is the ability to iteratively guess each value in a cell and backtrack if the placement fails.
public static int FindWorkingCell(SudokuPuzzle puzzle)
{
int minCandidates = puzzle.Cells.Where(cands => cands.Length >= 2).Min(cands => cands.Length);
return Array.FindIndex(puzzle.Cells, c => c.Length == minCandidates);
}
public static SudokuPuzzle Solve(SudokuPuzzle input)
{
if (input.Cells.All(cell => cell.Length == 1))
return input; //Hooray! Puzzle is solved!
int ActiveCell = FindWorkingCell(input);
foreach (int guess in input.Cells[ActiveCell])
{
SudokuPuzzle puzzle;
if ((puzzle = PlaceValue(input, ActiveCell, guess)) != null)
if ((puzzle = Solve(puzzle)) != null)
return puzzle;
}
return null;
}
FindWorkingCell decides which cell we want to try to iterate through. This could just be the first non-solved cell (at least 2 candidates) in the puzzle, but we can make a performance enhancement as Peter describes. We want to find an unsolved cell with the minimum number of remaining candidates. Guessing in a cell with 2 candidates gives us a 50% chance at guessing right and coming to a solution, while guessing in a cell with say 8 candidates leaves only a 12.5% chance.
Then the Solve function contains the logic to guess and backtrack. First it checks for the happy case that the puzzle is already fully solved. The foreach loop then guesses each candidate for the chosen cell. If we can PlaceValue it without contradiction, and then recurse on Solve without contradiction (the recursion to Solve will find a new cell and try the same stuff), then the puzzle is solved and we happily return it. Or if a guess fails, move on to guessing the next candidate. If all the guesses fail, we were already at a dead end before this call even started. So we return null, in which case the prior layer of Solve will reject its guess and try another candidate.
That's all we need! I added a simple console output routine, which isn't worth going into here. Let's give it a spin, using the easy puzzle from Peter Norvig's example.
var p = new SudokuPuzzle("..3.2.6..9..3.5..1..18.64....81.29..7.......8..67.82....26.95..8..2.3..9..5.1.3..");
p = SudokuPuzzle.Solve(p);
SudokuPuzzle.Output(p);
4 8 3 | 9 2 1 | 6 5 7
9 6 7 | 3 4 5 | 8 2 1
2 5 1 | 8 7 6 | 4 9 3
------+-------+------
5 4 8 | 1 3 2 | 9 7 6
7 2 9 | 5 6 4 | 1 3 8
1 3 6 | 7 9 8 | 2 4 5
------+-------+------
3 7 2 | 6 8 9 | 5 1 4
8 1 4 | 2 5 3 | 7 6 9
6 9 5 | 4 1 7 | 3 8 2
There we are, got the same solution as Mr. Norvig's program. Let's crystallize this as a test method too.
public static void SimpleTest()
{
var p = new SudokuPuzzle("..3.2.6..9..3.5..1..18.64....81.29..7.......8..67.82....26.95..8..2.3..9..5.1.3..");
p = SudokuPuzzle.Solve(p);
Debug.Assert(p.Cells.Select(c => c[0]).SequenceEqual(new int[] {
4, 8, 3, 9, 2, 1, 6, 5, 7, 9, 6, 7, 3, 4, 5, 8, 2, 1, 2, 5, 1, 8, 7, 6, 4, 9, 3,
5, 4, 8, 1, 3, 2, 9, 7, 6, 7, 2, 9, 5, 6, 4, 1, 3, 8, 1, 3, 6, 7, 9, 8, 2, 4, 5,
3, 7, 2, 6, 8, 9, 5, 1, 4, 8, 1, 4, 2, 5, 3, 7, 6, 9, 6, 9, 5, 4, 1, 7, 3, 8, 2
}));
}
I also added another couple constructors to round things out, which that test used.
public SudokuPuzzle(int[] input) : this((int)Math.Sqrt(input.Length))
{
for (int i = 0; i < input.Length; i++)
if (input[i] > 0 && input[i] <= Length)
{
var puzzle = PlaceValue(this, i, input[i]);
if (puzzle == null)
throw new ArgumentException("This puzzle is unsolvable!");
this.Cells = puzzle.Cells;
}
}
}
public SudokuPuzzle(string input) : this(input.Select(c => Char.IsDigit(c) ? c - '0' : 0).ToArray())
{
}
The first of these takes an integer array as a set of 81 clues. It starts with an unconstrained SudokuPuzzle object (by chaining to another constructor), then applies the clues to constrain the cells' candidate lists appropriately, ignoring zeroes. This is inherently an iterative stateful operation and so doesn't lend itself well to LINQiness, so we've got some looping. It makes use of the previously defined PlaceValue, and throws an exception if the provided clues create a contradiction. (A constructor must throw to abort, it can't return null.)
The last constructor takes a string to represent a puzzle. A digit represents a clue and any other character represents a blank cell. This constructor LINQ-magicks the string into integers and chains to the previous constructor.
A capability I want that the above algorithm can't do is find multiple solutions, or at least determine if they exist. Solve() collapses the recursion stack as soon as it hits its first success. It would be possible to enhance Solve() to keep track of the number of solutions found and return it along with the solved puzzle. But I don't want to pollute the pure function of Solve with some inelegant state. And the C# syntax for returning multiple values is clunky, needing a Tuple object or a full-blown class structure. What I really want is the ability for Solve to tell its caller when it has found a solution but then keep going. C# is wonderfully expressive as a language - we can do that very directly by passing a callback action into Solve!
public static List<SudokuPuzzle> MultiSolve(SudokuPuzzle input)
{
var Solutions = new List<SudokuPuzzle>();
Solve(input, p => Solutions.Add(p));
return Solutions;
}
public static SudokuPuzzle Solve(SudokuPuzzle input, Action<SudokuPuzzle> SolutionFunc = null)
{
if (input.Cells.All(cell => cell.Length == 1))
{
if (SolutionFunc != null)
{
SolutionFunc(input);
return null;
}
else
return input;
}
int ActiveCell = FindWorkingCell(input);
foreach (int guess in input.Cells[ActiveCell])
{
SudokuPuzzle puzzle;
if ((puzzle = PlaceValue(input, ActiveCell, guess)) != null)
if ((puzzle = Solve(puzzle, SolutionFunc)) != null)
return puzzle;
}
return null;
}
My new function MultiSolve() has the ability to return a List of all solutions to a Sudoku puzzle. Solve() now optionally takes a callback function, and MultiSolve() gives it one with that lambda expression p => Solutions.Add(p). So whenever Solve finds a solution, it can call that anonymous method. The closure adds the solution to the list back in the context of MultiSolve, and then Solve keeps on trucking looking for more solutions. This is very elegant, keeping both MultiSolve and Solve as pure functions while allowing state to propagate out of Solve.
Let's test it.
| 4 5 6 | 7 8 9
6 7 9 | 8 1 3 | 2 4 5
5 4 8 | 9 2 7 | 1 3 6
------+-------+------
| 5 9 4 | 6 7 8
8 5 7 | 3 6 1 | 4 9 2
9 6 4 | 7 8 2 | 5 1 3
------+-------+------
| 6 4 8 | 9 5 7
7 9 6 | 1 3 5 | 8 2 4
4 8 5 | 2 7 9 | 3 6 1
This puzzle has multiple solutions. Choose any of the boxes in the left column, and the missing 1 2 3 can go in any order for six combinations. Choose another box and there are two combinations left for it. So there should be 12 solutions to this puzzle. Can we find them?
public static void MultiSolveTest()
{
var puzzle = new SudokuPuzzle(" 456789679813245548927136 594678857361492964782513 648957796135824485279361");
var solutions = SudokuPuzzle.MultiSolve(puzzle);
Debug.Assert(solutions.Count() == 12);
}
Sure can.
An enhancement to this line of thinking is to create the ability to stop after a certain number of solutions, most commonly 2. Maybe we just want to know if multiple solutions exist but we don't really care how many. We can modify that callback to return a boolean, giving MultiSolve() the ability to tell Solve() to stop after a specified number of solutions and giving Solve() the ability to act on it.
public static ListMultiSolve(SudokuPuzzle input, int MaximumSolutions = -1) { var Solutions = new List (); Solve(input, p => { Solutions.Add(p); return Solutions.Count() < MaximumSolutions || MaximumSolutions == -1; }); return Solutions; } public static SudokuPuzzle Solve(SudokuPuzzle input, Func<SudokuPuzzle, bool> SolutionFunc = null) { if (input.Cells.All(cell => cell.Length == 1)) return (SolutionFunc != null && SolutionFunc(input)) ? null : input; ... //the rest of Solve is unchanged from before }
Solve continues doing its work as long as SolutionFunc returns true, which is as long as MultiSolve hasn't found the maximum number of solutions yet. (We can also omit MaximumSolutions or pass -1, which will cause the functions to keep running until they exhaust all solutions.)
var puzzle = SudokuPuzzle.Read(" 456789679813245548927136 594678857361492964782513 648957796135824485279361");
var solutions = SudokuPuzzle.MultiSolve(puzzle, 2);
solutions.ForEach(p => SudokuPuzzle.Output(p));
1 2 3 | 4 5 6 | 7 8 9
6 7 9 | 8 1 3 | 2 4 5
5 4 8 | 9 2 7 | 1 3 6
------+-------+------
2 3 1 | 5 9 4 | 6 7 8
8 5 7 | 3 6 1 | 4 9 2
9 6 4 | 7 8 2 | 5 1 3
------+-------+------
3 1 2 | 6 4 8 | 9 5 7
7 9 6 | 1 3 5 | 8 2 4
4 8 5 | 2 7 9 | 3 6 1
1 2 3 | 4 5 6 | 7 8 9
6 7 9 | 8 1 3 | 2 4 5
5 4 8 | 9 2 7 | 1 3 6
------+-------+------
3 1 2 | 5 9 4 | 6 7 8
8 5 7 | 3 6 1 | 4 9 2
9 6 4 | 7 8 2 | 5 1 3
------+-------+------
2 3 1 | 6 4 8 | 9 5 7
7 9 6 | 1 3 5 | 8 2 4
4 8 5 | 2 7 9 | 3 6 1
Testing this version with the previous puzzle shows that it works as intended, finding 2 solutions then stopping. (Notice the LINQy business even here in the output statement, writing out all the solutions with a single LINQ expression.) So now we have the ability to determine if multiple solutions exist to any Sudoku puzzle.
The next bit I want for my Sudoku toolkit is the ability to generate random puzzles. Peter Norvig's code could produce puzzles, but not in a great manner, creating puzzles with multiple solutions and occasionally even an unsolvable puzzle. I want the ability to properly generate a random puzzle with one and only one unique solution.
By the way, there are a lot of bad algorithms on the web for Sudoku generation! Many of them tell you to start with an existing grid and permute it by randomly exchanging rows or columns or numerals, or reflecting or rotating the whole puzzle. This creates only a very small subset of possible Sudoku grids! See here for the mathematics of Sudoku symmetry groups.
Here's my GOOD algorithm. I believe this will produce all unique Sudoku grids with equal probability, aside from any biases in the random number generator.
Of course, the last bit is why I wanted the ability to detect multiple solutions. This is an inherently stateful operation and doesn't lend itself well to LINQ magic, so here it is with some looping.
public static SudokuPuzzle RandomGrid(int size)
{
SudokuPuzzle puzzle = new SudokuPuzzle(size);
var rand = new Random();
while (true)
{
int[] UnsolvedCellIndexes = puzzle.Cells
.Select((cands, index) => new { cands, index }) //Project to a new sequence of candidates and index (an anonymous type behaving like a tuple)
.Where(t => t.cands.Length >= 2) //Filter to cells with at least 2 candidates
.Select(u => u.index) //Project the tuple to only the index
.ToArray();
int cellIndex = UnsolvedCellIndexes[rand.Next(UnsolvedCellIndexes.Length)];
int candidateValue = puzzle.Cells[cellIndex][rand.Next(puzzle.Cells[cellIndex].Length)];
SudokuPuzzle workingPuzzle = PlaceValue(puzzle, cellIndex, candidateValue);
if (workingPuzzle != null)
{
var Solutions = MultiSolve(workingPuzzle, 2);
switch (Solutions.Count)
{
case 0: continue;
case 1: return Solutions.Single();
default:
puzzle = workingPuzzle;
break;
}
}
}
}
I squeezed in a bit of LINQ anyway in that statement to find the list of all cells not yet solved. (We won't go into the details of it here.) The rest is straightforward. Make a working copy of the puzzle object to attempt placing this value into, then look for solutions. 0 solutions means we dump the working copy and try again; 1 solution means we're done; 2 solutions means we keep the working copy and continue trying.
var puzzle = SudokuPuzzle.RandomGrid(9); SudokuPuzzle.Output(puzzle); 5 9 1 | 7 8 2 | 3 4 6 4 6 7 | 9 5 3 | 8 1 2 3 8 2 | 1 6 4 | 7 9 5 ------+-------+------ 8 1 5 | 6 3 9 | 4 2 7 9 7 3 | 4 2 1 | 5 6 8 6 2 4 | 5 7 8 | 9 3 1 ------+-------+------ 1 3 8 | 2 9 7 | 6 5 4 2 5 9 | 8 4 6 | 1 7 3 7 4 6 | 3 1 5 | 2 8 9
There we go, a random grid. How can we test this? Obviously we won't get a recurring matchable output from a function that includes randomization. But we can test that every cell gets reduced to one candidate, and that the resulting solution can be used to initialize a new SudokuPuzzle object. (If we get a bad random grid, say two of the same number in a row, this will fail.)
public static void RandomGridTest()
{
var puzzle = SudokuPuzzle.RandomGrid(9);
Debug.Assert(puzzle.Cells.All(c => c.Length == 1));
var puzzle2 = new SudokuPuzzle(puzzle.Cells.Select(c => c.Single()).ToArray());
}
Creating a human-solvable puzzle from this is easy. Repeatedly depopulate cells at random, or perhaps in a pleasingly symmetric pattern. Check at each step that there is still one and only one solution, rejecting the depopulation if not. Continue as long as you like, adjusting the difficulty of the puzzle by the number of blank cells, to the theoretical minimum of 17 remaining clues. I won't detail this here.
Let's see how fast this is, using Peter Norvig's top95.txt file of hard puzzles. Just for kicks I wrote this test with LINQ also, using a .Select expression to transform a list of puzzles into the time taken to solve each. (I fully admit that this construct is less clear than simply looping, but more fun.) It's interesting how the compiler infers that times is a list of TimeSpan objects even though I never declared any usage of that type, just from the expression returned inside the lambda, that subtracting two DateTimes gives you a TimeSpan.
public static void Top95TimedTest()
{
var stream = new StreamReader("top95.txt");
var puzzles = new List<String>();
while (!stream.EndOfStream)
puzzles.Add(stream.ReadLine());
stream.Close();
var times = puzzles.Select(p =>
{
DateTime start = DateTime.Now;
var puz = SudokuPuzzle.Solve(new SudokuPuzzle(p));
return (DateTime.Now - start);
}).ToList();
Console.WriteLine("Average: " + times.Average(ts => ts.TotalSeconds));
Console.WriteLine("Worst: " + times.Max(ts => ts.TotalSeconds));
}
Average: 1.02680921052632
Worst: 16.515625
Yikes. Over a full second per puzzle and 16 seconds for the worst, compared to PN's average of 0.04 and max of 0.18. I expect my LINQ integer array operations to be a bit slower than the Python string manipulation, but not by that much. We gotta speed this up. But I'm not going to do it by blindly guessing where my program is slow. Visual Studio 2010 has a facility built in to do performance profiling and analysis. Here's what I got.

Holy crap, 66% of my time is spent in a single LINQ .ToArray expression. Given that IsPeer also shows up, it looks like this is our culprit.
public int[] Peers(int cell)
{
return Enumerable.Range(0, Length * Length).Where(c => IsPeer(cell, c)).ToArray();
}
That guy iterates over the entire puzzle every time it is called, meaning every time we ask for the list of peers of a cell. A little bit of memoization should clear that right up. (I knew all along that this would happen. I'm illustrating the point that LINQ makes it very easy to accidentally repeat expensive calculations, and also illustrating use of the VS tool to find this.)
//Dictionary to memoize lists of peers
//The key is a tuple of <int, int>, where the first value is the length of the puzzle (typically 9) and the second value is the cell index
private static Dictionary<Tuple<int, int>, int[]> _savedPeers = new Dictionary<Tuple<int, int>, int[]>();
public int[] Peers(int cell)
{
var key = new Tuple<int, int>(this.Length, cell);
if (!_savedPeers.ContainsKey(key))
_savedPeers.Add(key, Enumerable.Range(0, Length * Length).Where(c => IsPeer(cell, c)).ToArray());
return _savedPeers[key];
}
Are we faster now?
Average: 0.843092105263158 Worst: 13.59375
Hmm, not much better. Looks like the bottleneck around Peers was only that 11% of the original running time, not the monster 66%. Digging deeper in Visual Studio's performance analysis:
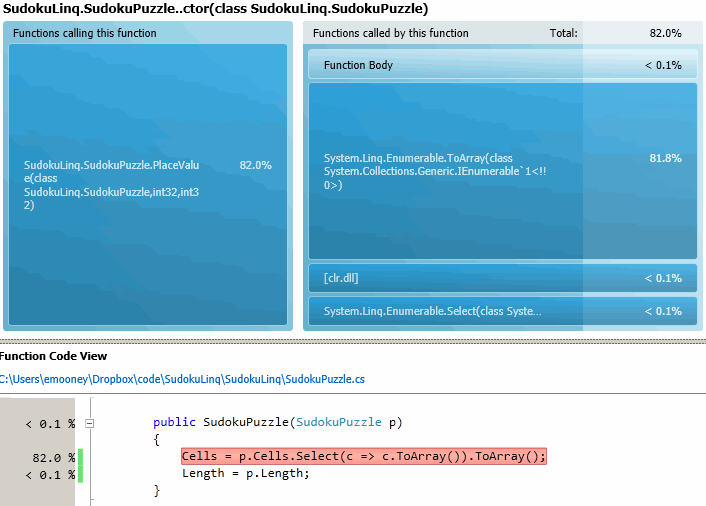
That's the copy constructor. Holy crap, 82% of my time is spent merely copying SudokuPuzzle objects! Well, let's try rewriting that constructor with some more explicit copy instructions rather than LINQ.
//Old slow version
//Cells = p.Cells.Select(c => c.ToArray()).ToArray();
Cells = new int[p.Cells.Length][];
for (int i = 0; i < Cells.Length; i++)
{
Cells[i] = new int[p.Cells[i].Length];
Buffer.BlockCopy(p.Cells[i], 0, this.Cells[i], 0, p.Cells[i].Length * sizeof(int));
}
Average: 0.327631578947368 Worst: 5.296875
Sure enough, that cut the running time drastically, about 2.5x faster. I do not understand why that original Select().ToArray operation was so much slower, but that is indeed a common occurrence for LINQ stuff. Performance analysis still shows 41% of the time in that Buffer.BlockCopy instruction, but that operation can't go faster without some rather extreme measures like calling out to a C++ DLL to do a direct memcopy.
The real solution would be a smarter algorithm for PlaceValue that doesn't need to copy 81 cells worth of the puzzle object all the time. Instead, it could mutate the original object and keep track of whatever few cells it changes, then revert them if a solving dead end is hit. But that approach strikes me as rather kludgy, where the function pretends purity but is really getting rather dirty under the sheets. I'd do it if necessary for production code, but it's beyond the scope of my toy program here.
That's all! The code is hosted on my Github for public access. Written in Visual C# 2010 Express, and should run in other versions.
- Erik Mooney